本文共 1367 字，大约阅读时间需要 4 分钟。

一、数组

1、定义

• 数组是由 n(n>=1) 个相同类型的元素构成的有限序列，每个元素在 n 个线性关系中的序号称为该元素的下标，下标的取值范围称为数组的维界。

2、与线性表的关系

• 数组可以视为线性表的推广，一维数组就是一个线性表，二维数组则是一个元素为定长线性表的线性表，以此类推。
• 数组一旦定义，其维数和维界便固定下来了，除去结构的初始化和销毁，数组只能对元素进行存取和修改操作。

3、存储结构

• 绝大多数的高级编程语言都对数组这一数据结构进行了支持，数组在内存中占用连续的一段存储空间，其大小是单个元素的存储大小与元素个数的乘积。
• 一维数组与存储结构的关系式为：
  
• 其中的 L 就是数组元素所占的存储单元。
• 多维数组有按行优先和按列优先两种映射方法。按行优先就是对数组元素进行存储时，先行后列，先存储行号小的元素，行号相等的先存储列号较小的元素。按列优先，就是先列后行，列号小的元素先存储，列号相等的先存储行号小的元素。

二、特殊矩阵的压缩存储

• 在编程中，由于数组和矩阵的逻辑结构很相似，我们通常采用数组来描述矩阵，一个一维矩阵对应一个一维数组，二维矩阵对应二维数组……以此类推。

1、特殊矩阵

• 特殊矩阵：指具有许多相同元素或零元素，并且这些相同元素或零元素的分布具有一定规律性的矩阵。
• 常见的特殊矩阵有：对称阵、上三角阵、下三角阵、对角阵。
• 通常对这些特殊矩阵进行存储时，并不是采用通常的n:n的映射关系，而是采用压缩存储；所谓矩阵的压缩存储：根据特殊矩阵中值相同的元素的分布规律，并根据规律将这些矩阵元素存储到一个存储空间中。

2、对称阵

• 所谓对称矩阵，就是在矩阵中以主对角线（从左上到右下）分界线，右上半部分的矩阵沿主对角线翻折后，可以和左下半部分的矩阵元素一一对应。此时若仍旧采用二维数组存放，则或造成一半存储空间的浪费。
• 出于节省存储空间考虑，通常采用长度为 n(n+1)/2 的一维数组来存放对称二维矩阵，并且在数组中的下标 k 与 矩阵的 (i,j) 的对应关系如下：
  

3、三角阵

• 三角阵分为下三角矩阵和上三角矩阵，其形状分别如下：

  

• 因此三角阵的存储思想与对称阵类似，将元素不重复的存储在一个B[n(n+1)/2+1] 的一维数组中。

• 下三角矩阵的矩阵元素下标与一维数组的下标的对应关系如下：

  
  

• 上三角矩阵元素与数组元素的下标对应关系：

  
  

3、三对角矩阵

• 对角矩阵也称带状矩阵，对于n阶方阵 A 的任意个元素，当|i-j|>1 时，其值为 0，则称为三对角阵，其形状如下：
  
• 三对角阵的压缩存储，就是将三条对角线上的元素按行优先方式存储在一维数组 B 中，且规定 a00 存放在 B[0] 中，其余矩阵元素与数组元素的下标关系：k=2i+j-3。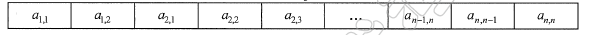
  

4、稀疏矩阵

• 矩阵中非零元素的个数 t，相对矩阵元素的个数 s 来说非常少，即 s>> t 的矩阵就称为稀疏矩阵。

• 但是由于这些非零元素的分布找不到一个线性规律，因此前面几种方法——只存储非零元素的方法都行不通。

• 对稀疏矩阵进行压缩存储的普遍方法，时用非零元素及其所在行标和列标构成一个三元组：(行标，列标，值)，然后再按照某种规律存储这些三元组。可以采用数组存储三元组，也可以用十字链表法存储。

  

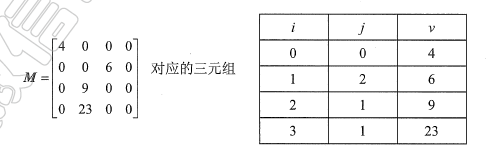
• 值得注意的是：稀疏矩阵压缩存储后失去了随机存取特性。

转载地址：http://lqqgn.baihongyu.com/